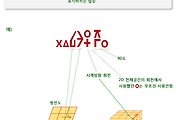
바로 앞글에 소개했던 2D 회전을 숙지했다면 이번 3D 회전은 어렵지 않다. 연장선상에 있는 내용이기 때문이다. 쉽게 말해서, 3D 공간에 있는 형태가 어느 축을 기준으로 얼마만큼의 각도로 회전하느냐가 관건이다.
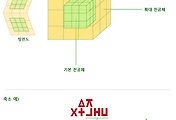
형태가 제자리에서 회전을 할 수도 있고 전공체의 중심(2행2열)으로 이동해서 회전할 수도 있다(2D와 같은 맥락). 어쨌튼 그 회전은 3D 공간상의 어떤 축(형태의 중심을 지나는 축)을 기준으로 하여 회전을 한다. 톨글로 그 축을 표기해주는 것만이 3D에서 추가되는 항목이다. 나머지는 2D 회전이동과 동일한 내용이다.
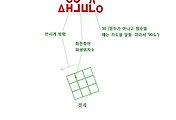
그 회전축은 운체(운동소 2개)로 표기할 수 있다. 쉽게 말해서 이 회전축은 지구의 북극에서 남극으로 관통하는 직선과 같다고 말할 수 있다. 그 직선을 축으로 하여 지구가 자전을 하는 것처럼 3D 공간상의 형태가 회전을 한다. 회전이 시계방향인지 반시계방향인지도 북극에서 바라봤을 때(회전축이 형태의 중심을 관통해들어가기 시작한 지점)를 기준으로 생각하기로 한다.(이하 그림설명 참조)
한편, 2D 회전에 관한 내용은 바로 앞에 올린 '2D 회전' 글을 참고하면 될 것이다. (이하 그림설명 참조)
참고글: 2차원 회전이동 (수정됨)
2012년 2월 16일 김곧글(Kim Godgul)

'톨글(Tolgul)' 카테고리의 다른 글
| [3차원 톨글] 전공체(3x3Cube)의 회전 (0) | 2012.02.19 |
|---|---|
| 전체공간(3x3Grid)의 회전 (0) | 2012.02.17 |
| 2차원 회전이동 (수정됨) (0) | 2012.02.15 |
| [3차원 톨글] 전공체(3x3cube) 체적의 확대/축소 (0) | 2012.02.13 |
| 전체공간의 확대/축소 (0) | 2012.02.12 |