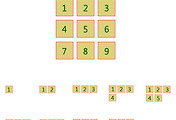
앞서 소개한 ‘확률이동’과 마찬가지로 ‘멀티박스’를 어떻게 해석하느냐의 관점에서 ‘어중간한 이동’이다. ‘멀티박스’라는 것은 어떻게 표기한다는 표기법에 관한 내용이고, ‘확률이동’과 ‘어중간한 이동’은 멀티박스로 표기한 문자를 어떻게 해석하는 지에 관한 내용이다. 따라서 멀티박스로 표기한 동글 글자를 확률이동 내용으로 해석할 수도 있고, 어중간한 이동으로 해석할 수도 있다는 얘기다. 또는 나중에 다른 내용이 추가될 수도 있을 것이다.
‘어중간한 이동’은 모호한 지점들 간의 이동을 말한다. 이제까지 다뤘던 3x3x3 정육면체에서의 이동은 반드시 3x3x3 정육면제 속 작은 박스의 이동이었다. 만약 작은 박스와 박스 사이 중간 지점에서 출발하고 도착하는 이동을 표기하고 싶다면 어떻게 할까? 한편, 이런 생각이 반드시 옳지도 않고 필요하지도 않다고 비판 받을 수도 있다. 왜냐하면 3x3x3 정육면체는 추상적인 공간을 말하는 것이므로 그 작은 박스들 사이의 중간지점을 생각하는 것 자체가 부적합하다고 볼 수 있기 때문이다. 아무튼 작은 박스와 박스 또는 여러 개의 박스의 중간지점(전체 면적의 중간 또는 무게 중심)을 다룬다는 전제 하에 멀티박스로 표기된 동글 문자를 어중간한 이동으로 해석할 수 있다.
실생활에서 가장 쉽게 적용해볼 수 있는 것이 야구에서 투수가 던진 공이 타자와 포수 앞에서 즉 홈플레이트(home plate) 위에서 어떻게 움직이는지를 생각해 보는 것이다. 이때 야구공이 가상적으로 홈플레이트 위에 그려놓은 3x3x3 정육면체의 작은 박스를 따라 정확히 이동하지는 않을 것이다. 작은 박스와 박스 사이 어중간한 지점에서 지점으로 이동하는 경우가 훨씬 많을 것이다. 한편, 정확하고 정교하게 다루자면 한도 끝도 없을 것이고 이곳에서 즉 동글이라는 문자체계가 다룰 수 있는 영역을 벗어난다. 대략적으로 3x3x3 정육면체 작은 박스와 박스 사이 중간지점 정도의 정밀도만을 다루는 것이 어중간한 이동이라고 볼 수 있다.
이것은 확률이동만큼 복잡한 내용이 들어있는 것은 아니다. 예를 들어, 다초박스에 두 개의 박스가 있다면 그 두 개 박스의 중간지점이 출발점이 되는 것이다. 다종박스에 세 개의 박스가 있다면 그 세 개 박스의 중간지점이 도착점이 되는 것이다. 이처럼 멀티박스로 표기된 동글을 어중간한 이동으로 해석할 수 있다.
2016년 12월 30일 김곧글(Kim Godgul)
'동글(Dongul)' 카테고리의 다른 글
| 동글(Dongul) - 출발점에 S좌표, R좌표 사용한다는 표기의 단축형 (0) | 2017.01.12 |
|---|---|
| 동글(Dongul) - 어떤 이동을 동글로 모두 쓰기 (0) | 2017.01.11 |
| 동글(Dongul) - 멀티박스: 확률이동 (중요) (0) | 2016.10.31 |
| 동글(Dongul) - 멀티박스(Multi Box) (0) | 2016.10.23 |
| 동글(Dongul) - 역방향 이동 (reverse move) (0) | 2016.10.19 |